一、教学目标

1.知道什么是圆周运动，什么是匀速圆周运动。

2.知道线速度的物理意义、定义式、矢量性，知道匀速圆周运动线速度的特点。

3.知道角速度的物理意义、定义式及单位，了解转速和周期的意义。

4.掌握线速度和角速度的关系，掌握角速度与转速、周期的关系。

5.能在具体的情景中确定线速度和角速度与半径的关系。

二、核心素养

物理观念：

通过对圆周运动知识的学习，培养学生对同一问题多角度进行分析研究的物理观念。

科学思维：

通过极限思想和数学知识的应用，体会学科知识间的联系，建立普遍联系的观点。

科学探究：

通过课堂演示实验的观察，引导学生归纳总结描述物体做圆周运动快慢的方法，进而引出描述物体做圆周运动快慢的物理量。

科学态度与责任：

经历观察、分析总结、及探究等学习活动，培养学生尊重客观事实、实事求是的科学态度。

自主探究（一）　线速度、角速度和匀速圆周运动

■情境导入

闹钟与手表为什么会有上述快慢之争？提出你的看法，请同学进行讨论。

【答案】　“闹钟”和“手表”是从不同角度看圆周运动的快慢，闹钟指的是秒针针尖的线速度；手表则指的是秒针转动的角速度。

■归纳拓展

1.线速度v

(1)物理意义：描述质点沿圆周运动的快慢。

(2)定义：做圆周运动的物体通过的弧长Δs和所用时间Δt的比值叫作线速度。

(3)大小：v＝。单位：m/s。

(4)线速度是矢量。

2.角速度

(1)意义：描述做圆周运动的物体绕圆心转动的快慢。

(2)大小：ω＝＝。

单位：弧度每秒，符号是rad/s。

(3)匀速圆周运动是角速度不变的运动。

3.匀速圆周运动

(1)匀速圆周运动：质点沿圆周运动，在任意相等的时间里通过的圆弧长度都相等的运动叫作匀速圆周运动。

(2)方向：圆周运动线速度的方向总是沿该点圆周的切线方向，如图所示。

(3)性质：由于物体做匀速圆周运动时的速度方向不断发生变化，所以匀速圆周运动是一种变速运动。

【例1】 做匀速圆周运动的物体，10 s内沿半径为20 m的圆周运动了100 m，试求物体做匀速圆周运动时：

(1)线速度的大小；(2)角速度；(3)周期。

【答案】　(1)10 m/s　(2)0.5 rad/s　(3)4π s

【解析】　(1)根据线速度的定义式v＝可得

v＝ m/s＝10 m/s。

(2)根据v＝ωr可得，ω＝＝ rad/s＝0.5 rad/s。

(3)T＝＝ s＝4π s。

【针对训练1】 下面关于匀速圆周运动的表述正确的是(　　)

A.做匀速圆周运动的物体处于平衡状态

B.匀速圆周运动的线速度是恒定不变的

C.做匀速圆周运动的物体，其运动快慢用线速度描述

D.做匀速圆周运动的物体，在任意相等时间内的位移相同

【答案】　C

【解析】　做匀速圆周运动的物体，其线速度方向是时刻变化的，所受合力不为零，因此处于非平衡状态，故A错误；做匀速圆周运动的物体，线速度的方向总是在该点的切线方向，时刻是变化的，物体运动快慢可用线速度描述，故B错误，C正确；做匀速圆周运动的物体在任意相等时间内通过的弧长即路程相等，但位移的方向可能不同，故D错误。

自主探究（二）　描述圆周运动的物理量及关系

1.物理量的比较

2.线速度与角速度的关系

(1)“控制变量法”分析物理量间的关系

①当半径r一定时，线速度v与角速度ω成正比。

②当角速度ω一定时，线速度v与半径r成正比。

③当线速度v一定时，角速度ω与半径r成反比。

(2)图像法表示物理量间的关系

【例2】 (2021·广西梧州市高一期中)如图是一种叫“指尖陀螺”的玩具。当将陀螺绕位于中心A的转轴旋转时，陀螺上B、C两点的周期、角速度及线速度的关系正确的是(　　)

A.T_B＝T_C，v_B<v_C        B.T_B>T_C，v_B<v_C

C.ω_B＝ω_C，v_C<v_B       D.ω_B>ω_C，v_B<v_C

【答案】　A

【解析】　由于是同轴转动，可知ω_B＝ω_C，根据T＝，得转动周期相等，即T_B＝T_C，根据v＝rω，因为r_B<r_C，则v_B<v_C，故B、C、D错误，A正确。

【针对训练2】 (2021·甘肃靖远二中高一期中)如图所示是一个玩具陀螺。a、b、c是陀螺上的三个点。当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时，下列表述正确的是(　　)

A.a、b、c三点的线速度大小相等

B.a、b、c三点的角速度相等

C.a、b的角速度比c的角速度大

D.c的线速度比a、b的线速度大

【答案】　B

【解析】　a、b、c三点的角速度相同，而线速度不同，由v＝ωr得v_a＝v_b>v_c，选项B正确，A、C、D错误。

自主探究（三）　两类传动模型问题

1.同轴传动模型

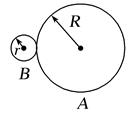
如图所示，A点和B点在同轴的一个“圆盘”上，它们的半径分别为r和R，且r＜R。运动的特点是转动角速度相同，转动方向相同，即同为逆时针转动或顺时针转动，转动周期相同，转动线速度v_A＜v_B。

2.“皮带传动类”模型

(1)三类典型传动(如图所示)

　

        ①皮带传动　　　　　②齿轮传动

     ③摩擦传动

(2)共同特点

齿轮传动、皮带传动、摩擦传动方式均有接触处的线速度大小相等的特点。

【例3】 (2021·黑龙江哈尔滨三中高一月考)如图所示为常见的自行车传动示意图。A轮与脚蹬子相连，B轮与车轴相连，C为车轮。当人蹬车匀速运动时，以下说法中正确的是(　　)

A.A轮与B轮的角速度相同

B.A轮边缘的线速度比B轮边缘的线速度大

C.B轮边缘与C轮边缘的线速度大小相同

D.B轮与C轮的角速度相同

【答案】　D

【解析】　A轮与B轮边缘上的点与传动链条接触，其速度大小和传动链条的速度大小一致，所以A轮边缘与B轮边缘的线速度大小相等，根据公式v＝rω可知线速度相等时，半径小的角速度大，所以A轮角速度小于B轮的角速度，故A、B错误；B轮与C轮在同一个轮子上，所以B轮边缘与C轮边缘的角速度相同，根据公式v＝ωr可知角速度相同时，半径小的线速度小，所以B轮边缘的线速度小于C轮边缘的线速度，故C错误，D正确。

【针对训练3】 (2021·浙江高一月考)如图甲所示，修正带是通过两个齿轮的相互咬合进行工作的，其原理可简化为图乙所示。A、B是盘上的边缘点，C为A盘上的一点，已知2r_C＝r_A，r_C＝r_B。以下关于A、B、C三点的线速度大小v、角速度大小ω之间关系的说法正确的是(　　)

A.v_A<v_B，ω_A＝ω_B          B.v_A>v_C，ω_A＝ω_C

C.ω_A>ω_B，v_B＝v_C          D.ω_A<ω_B，v_B＝v_C

【答案】　B

【解析】　A、C是同轴传动，有ω_A＝ω_C，v_A＝ω_Ar_A，v_C＝ω_Cr_C，又因2r_C＝r_A，故v_A＝2v_C，B、A是同轴传动，有v_A＝v_B，又因v_A＝2v_C，所以v_B＝2v_C，故A、C、D错误，B正确。

1.(线速度和匀速圆周运动)质点做匀速圆周运动，在任意相等的时间内，下列物理量可能不同的是(　　)

A.通过的弧长           B.通过的位移大小

C.转过的角度           D.速度的变化

【答案】　D

【解析】　质点做匀速圆周运动时，因线速度的大小不变，故在任意相等的时间内通过的圆弧长度相同，A错误；位移是矢量，所以在任意相等的时间内通过的位移方向不一定相同，但是位移大小相等，B错误；质点做匀速圆周运动时，角速度是不变的，所以在任意相等的时间内转过的角度是相同的，C错误；速度的变化是矢量，任意相等的时间内的速度变化方向不一定相同，D正确。

2.(描述匀速圆周运动的物理量及关系)质点做匀速圆周运动时，下列说法中正确的是(　　)

A.因为v＝ωr，所以线速度v与圆周半径r成正比

B.因为ω＝，所以角速度ω与圆周半径r成反比

C.因为ω＝2πn，所以角速度ω与转速n成正比

D.因为ω＝，所以角速度ω与周期T成正比

【答案】　C

【解析】　ω一定时，线速度v与圆周半径r成正比，选项A错误；v一定时，角速度ω与圆周半径r成反比，选项B错误；在用转速或周期表示角速度时，角速度与转速成正比，与周期成反比，选项C正确，D错误。

3.(描述匀速圆周运动的物理量及关系)(2021·辽宁省实验中学高一期中)如图所示，小强同学正在荡秋千，关于绳上a点和b点的线速度和角速度，下列关系正确的是(　　)

A.v_a＝v_b            B.v_a＞v_b

C.ω_a＝ω_b           D.ω_a＜ω_b

【答案】　C

【解析】　绳子绕O点转动，a、b两点角速度相等，ω_a＝ω_b，D错误，C正确；因r_a＜r_b，故v_b＞v_a，A、B错误。

4.(两类传动模型) (2021·江苏苏州市高一期末)明代出版的《天工开物》一书中就有牛力齿轮翻车的图画(如图所示)，记录了我们祖先的劳动智慧，若A、B、C三齿轮半径的大小关系如图(r_A>r_B>r_C)，下列关于A、B、C的线速度和角速度的关系正确的是(　　)

A.线速度v_A＝v_B>v_CB.线速度v_A<v_B＝v_C

C.角速度ω_A<ω_B<ω_CD.角速度ω_A＝ω_B>ω_C

【答案】　A

【解析】　齿轮A与齿轮B是同缘传动，边缘点线速度相等，故v_A＝v_B，因为半径关系为r_A>r_B，根据公式v＝ωr可知，A的角速度小于B的角速度，即ω_A＜ω_B；B与C是同轴传动，角速度相等，即ω_C＝ω_B，所以角速度关系为ω_A＜ω_B＝ω_C，故C、D错误；B、C两轮角速度相等，根据公式v＝ωr可知，半径比较大的齿轮B比C边缘的线速度大，即v_C＜v_B，结合以上可得v_C＜v_B＝v_A，故A正确，B错误。