1.了解人们追寻守恒量和建立“能量”概念的漫长过程。

2.知道什么是机械能，知道物体的动能和势能可以相互转化。

3.能推导机械能守恒定律表达式。

4.会判断系统机械能是否守恒，能运用机械能守恒定律解决有关问题。

1.物理观念：功和机械能相关的初步能量观念。

2.科学思维：(1)守恒思想。

(2)能对熟悉物理情境建构物理模型。

3.关键能力：分析推理能力和物理建模能力。

自主探究（一）　机械能守恒的判断

1.研究对象

(1)当只有重力做功时，可取一个物体(其实是物体与地球构成的系统)作为研究

对象。

(2)当物体之间的弹力做功时，必须将这几个物体构成的系统作为研究对象(使这些弹力成为系统内力)。

2.守恒条件理解

(1)从能量转化分析，系统内部只发生动能和势能的相互转化，无其他形式能量(如内能)之间的转化，系统机械能守恒。

(2)从做功条件分析，机械能守恒的条件是只有重力或弹力做功。可从以下三种情形理解：

①只受重力作用：如在不考虑空气阻力的情况下的各种抛体运动(自由落体、竖直上抛、平抛、斜抛等)。

②受其他力，但其他力不做功，只有重力或弹力做功，例如：物体沿光滑的曲面下滑，受重力、曲面的支持力的作用，但曲面的支持力对物体不做功。

③有重力、弹簧弹力外的其他力做功，但是做功的代数和为零。

3.守恒的判断方法

(1)做功分析法(常用于单个物体)

(2)能量分析法(常用于多个物体组成的系统)

【例1】 (2021·苏州新草桥中学高一期中)关于机械能，下列说法正确的是(　　)

A.物体做竖直面内的圆周运动，机械能一定守恒

B.物体做匀速直线运动，机械能一定守恒

C.合力对物体做功为零时，物体的机械能一定守恒

D.只有重力对物体做功时，物体的机械能一定守恒

【答案】　D

【解析】　物体在竖直平面内做圆周运动，因为不清楚物体受力情况，若用轻杆连接的物体在竖直平面内做匀速圆周运动，则此时机械能不守恒，故A错误；物体做匀速直线运动，只能说明物体所受合力为0，不能确定是否满足机械能守恒条件，若人在电梯中匀速上升或下降，则机械能不守恒，故B错误；合力对物体做功为0时，物体的动能保持不变，但机械能不一定守恒，故C错误；只有重力做功，满足机械能守恒条件，故物体的机械能守恒，故D正确。

【针对训练1】 (2021·江苏如皋中学高一月考)如图所示，下列关于机械能是否守恒的判断正确的是(　　)

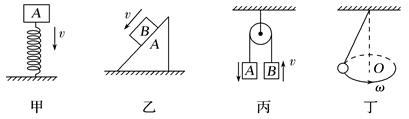
A.甲图中，物体A将弹簧压缩的过程中，A机械能守恒

B.乙图中，A置于光滑水平面，物体B沿光滑斜面下滑，物体B在下滑过程中机械能守恒

C.丙图中，不计任何阻力和定滑轮质量时A加速下落，B加速上升过程中，A、B的机械能均守恒

D.丁图中，小球沿水平面做圆锥摆匀速运动的过程中，小球的机械能守恒

【答案】　D

【解析】　甲图中在物体A压缩弹簧的过程中，弹簧和物体A组成的系统，只有重力和弹力做功，系统机械能守恒，对于A，由于弹簧的弹性势能在增加，则A的机械能减小，故A错误；乙图中物块B沿A下滑的过程中，A要向后退，A、B组成的系统，只有重力势能和动能的转化，机械能守恒，由于A的机械能增大，所以B的机械能在减小，不守恒，故B错误；丙图中对A、B组成的系统机械能守恒，但对单个物体来说，B的机械能增加，A的机械能减少，故C错误；丁图中小球在做圆锥摆匀速运动的过程中，重力势能和动能都不变，机械能守恒，故D正确。

自主探究（二）　机械能守恒定律的应用

■情境导入

如图，质量为m的小球从光滑曲面上滑下。当它到达高度为h₁的位置A时，速度的大小为v₁，滑到高度为h₂的位置B时，速度的大小为v₂。在由高度h₁滑到高度h₂的过程中(不计空气阻力，重力加速度为g)：

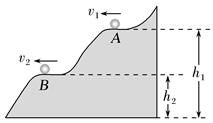
     研究小球的能量变化

(1)小球的重力势能减少了多少？

(2)小球的动能增加了多少？

(3)小球下滑过程中机械能守恒吗？若守恒，列出表达式。

(4)小球重力势能减少量等于动能的增加量吗？

【答案】　(1)重力势能的减少量为ΔE_p＝mgh₁－mgh₂

(2)动能增加量为ΔE_k＝mv－mv

(3)机械能守恒，表达式为mgh₁＋mv＝mgh₂＋mv

(4)由(3)变形可知mgh₁－mgh₂＝mv－mv，即小球重力势能减少量等于动能增加量

■归纳拓展

1.表达形式

2.基本思路

【例2】 (2021·上海市虹口区高一期中)2018年冬季奥林匹克运动会跳台滑雪比赛在韩国平昌举行。如图为一跳台的示意图。假设运动员从雪道的最高台A由静止开始滑下，不借助其他器械，沿光滑雪道到达跳台的B点时速度多大？当他落到离B点竖直高度为10 m的雪地C点时，速度又是多大？(设这一过程中运动员没有做其他动作，忽略摩擦和空气阻力，取g＝10 m/s²)

【答案】　8.9 m/s　16.7 m/s

【解析】　运动员在滑雪过程中只有重力做功，故运动员在滑雪过程中机械能守恒。取B点所在水平面为参考平面。由题意知A点到B点的高度差h₁＝4 m，B点到C点的高度差h₂＝10 m，从A点到B点的过程由机械能守恒定律得mv＝mgh₁

故v_B＝＝4 m/s＝8.9 m/s

从B点到C点的过程由机械能守恒定律得

mv＝－mgh₂＋mv

故v_C＝＝2 m/s＝16.7 m/s。

【针对训练2】 (2021·南平八中高一月考)如图所示，质量m＝60 kg的运动员以6 m/s的速度从高h＝8 m的滑雪场A点沿斜坡自由滑下，以最低点B为零势能面，g＝10 m/s²，一切阻力可忽略不计。求：

(1)运动员在A点时的机械能；

(2)运动员到达最低点B时的速度大小；

(3)运动员继续沿斜坡向上运动能到达的最大高度。

【答案】　(1) 5 880 J　(2)14 m/s　(3)9.8 m

【解析】　(1)运动员在A点时的机械能

E＝E_k＋E_p＝mv²＋mgh＝5 880 J。

(2)运动员从A运动到B的过程，根据机械能守恒定律得

E＝mv

解得v_B＝＝14 m/s。

(3)运动员从A运动到斜坡上最高点的过程，由机械能守恒定律得E＝mgh_m

解得h_m＝9.8 m。

自主探究（三）　非质点类物体的机械能守恒问题

1.在应用机械能守恒定律处理实际问题时，经常遇到像“链条”“液柱”类的物体，其在运动过程中将发生形变，其重心位置相对物体也发生变化，因此这类物体不能再看成质点来处理。

2.物体虽然不能看成质点来处理，但因只有重力做功，物体整体机械能守恒。一般情况下，可将物体分段处理，确定质量分布均匀的规则物体各部分的重心位置，根据初、末状态物体重力势能的变化列式求解。

【例3】 如图所示，长为L的均匀链条放在光滑水平桌面上，且使长度的垂在桌边，松手后链条从静止开始沿桌边下滑，则链条滑至刚刚离开桌边时的速度大小为(重力加速度大小为g)(　　)

A.               B. 

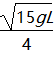C.               D.4

【答案】　C

【解析】　由机械能守恒定律得ΔE_p减＝ΔE_k增，即mg·L＋mg·L＝mv²，所以v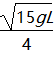＝。选项C正确。

【针对训练3】 如图所示，粗细均匀，两端开口的U形管内装有同种液体，开始时两边液面高度差为h，管中液柱总长度为4h，后来让液体自由流动，当两液面高度相等时，右侧液面下降的速度为(重力加速度大小为g)(　　 )

A.            B. 

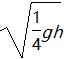C.            D.

【答案】　A

【解析】　当两液面高度相等时，减少的重力势能转化为全部液体的动能，根据机械能守恒定律得mg·h＝mv²，解得v＝，选项A正确。

1.(机械能守恒的判断)(2021·北京顺义区一中高一期中)下列所述的情景中，机械能守恒的是(　　)

A.汽车在平直路面上加速行驶

B.小球在空中做自由落体运动

C.降落伞在空中匀速下落

D.木块沿斜面匀速下滑

【答案】　B

【解析】　汽车在平直路面上加速行驶，说明汽车的牵引力在对汽车做功，所以汽车的机械能不守恒，故A错误；做自由落体运动的物体只受重力的作用，所以小球的机械能守恒，故B正确；降落伞在空中匀速下落，说明重力和空气的阻力大小相等，阻力做了负功，所以机械能不守恒，故C错误；木块沿斜面匀速下滑，说明此时的木块要受到沿斜面的摩擦力的作用，且对木块做了负功，所以其机械能不守恒，故D错误。

2.(机械能守恒定律的应用)(2021·山东济南外国语学校高一月考)如图所示，光滑斜面的顶端固定一弹簧，一物体向右滑行，并冲上固定在地面上的斜面。设物体在斜面最低点A的速度为v，压缩弹簧至C点时弹簧最短，C点距地面高度为h，则物体运动到C点时，弹簧的弹性势能是(　　)

A.mgh－mv²             B.mv²－mgh

C.mgh                    D.mgh＋mv²

【答案】　B

【解析】　由A到C的过程运用机械能守恒定律得

mgh＋E_p＝mv²

所以E_p＝mv²－mgh，故选项B正确。

3.(机械能守恒定律的应用) (2021·甘南藏族自治州一中高一期末)如图所示，将质量为m的石块从离地面h高处以初速度v₀斜向上抛出。以地面为参考平面，不计空气阻力，当石块落地时(　　)

A.动能为mv             B.机械能为mgh＋mv

C.动能为mgh             D.重力势能为mgh

【答案】　B

【解析】　不计空气阻力，石块的机械能守恒，机械能等于重力势能与动能之和，以地面为参考平面，落地时石块的重力势能为零，则石块落地时机械能等于动能，即E＝E_k＝mgh＋mv，故B正确，A、C、 D错误。

4.(非质点类物体的机械能守恒问题)如图所示，总长为L的光滑匀质铁链跨过一个光滑的轻质小滑轮，开始时下端A、B相平齐，当略有扰动时其一端下落，则当铁链刚脱离滑轮的瞬间，铁链的速度为多大？

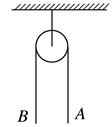
【答案】　

【解析】　方法一　取整个铁链为研究对象

设整个铁链的质量为m，初始位置的重心在A点上方L处，末位置的重心与A点最初位置在同一水平面上，则重力势能的减少量为ΔE_p＝mg·L

由机械能守恒定律得mv²＝mg·L，则v＝ 。

方法二　将铁链看作两段

铁链由初始状态到刚离开滑轮时，等效于左侧铁链BB′部分移到AA′位置。

重力势能减少量为

ΔE_p＝mg·

由机械能守恒定律得

mv²＝mg·

则v＝ 。