【知识目标】
1.知道如果一个力或几个力的合力的效果是使物体产生向心加速度,它就是圆周运动的物体所受的向心力。会在具体问题中分析向心力的来源。
2.能理解运用匀速圆周运动的规律分析和处理生产和生活中的具体实例。
3.知道向心力和向心加速度的公式也适用于变速圆周运动,会求变速圆周运动中物体在特殊点的向心力和向心加速度。
3.通过对匀速圆周运动的实例分析,渗透理论联系实际的观点,提高学生分析和解决问题的能力。
4.通过匀速圆周运动的规律也可以在变速圆周运动中使用,渗透特殊性和一般性之间的辩证关系,提高学生的分析能力。
5.通过对离心现象的实例分析,提高学生综合应用知识解决问题的能力。
6.通过对几个实例的分析,使学生明确具体问题必须具体分析,理解物理与生活的联系,学会用合理、科学的方法处理问题。
7.通过离心运动的应用和防止的实例分析。使学生明白事物都是一分为二的,要学会用一分为二的观点来看待问题。
8.养成良好的思维表述习惯和科学的价值观。
【素养目标】
1.科学思维
建立水平面内的转弯模型和竖直面内圆周运动模型分析实际问题。
2.关键能力:物理建模能力和分析推理能力。
自足探究(一) 火车或汽车转弯问题
1.弯道的特点:弯道处外高内低,但火车或汽车在行驶过程中,重心高度不变,即重心轨迹在同一水平面内,向心加速度和向心力均沿水平面指向圆心。
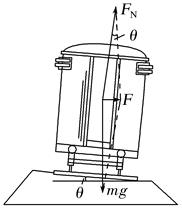
2.向心力的来源:车速合适时转弯所需的向心力完全由重力和支持力的合力提供,合力沿水平方向,大小F=mgtan θ。
3.转弯规定速度:若火车或汽车转弯时只受重力和支持力作用,则mgtan θ=m![]() ,可得转弯规定速度v0=
,可得转弯规定速度v0=![]() 。[R为弯道半径,θ为路轨平面(或路面)与水平面的夹角]
。[R为弯道半径,θ为路轨平面(或路面)与水平面的夹角]
4.轨道压力与火车速度的关系
(1)当火车行驶速度v等于规定速度v0时,所需向心力仅由重力和支持力的合力提供,此时火车对内、外轨道无挤压作用。
(2)当火车行驶速度v>v0时,外轨道对轮缘有侧压力。
(3)当火车行驶速度v<v0时,内轨道对轮缘有侧压力。
【例1】 火车转弯时,如果铁路弯道的内、外轨一样高,则外轨对轮缘(如图甲所示)挤压的弹力F提供了火车转弯的向心力(如图乙所示),但是靠这种办法得到向心力,铁轨和车轮极易受损。在修筑铁路时,弯道处的外轨会略高于内轨(如图丙所示),当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,以下说法中正确的是( )
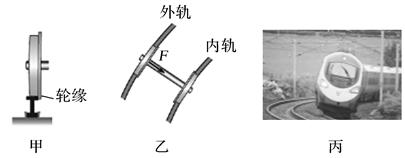
A.该弯道的半径R=![]()
B.当火车质量改变时,规定的行驶速度也将改变
C. 当火车速率大于v时,外轨将受到轮缘的挤压
D. 当火车速率小于v时,外轨将受到轮缘的挤压
【答案】 C
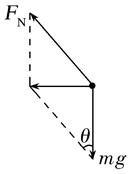
【解析】 对火车受力分析,如图所示,火车转弯时不侧向挤压车轮轮缘,由重力和支持力的合力提供向心力,设转弯处斜面的倾角为θ,根据牛顿第二定律得
mgtan
θ=m![]() ,解得R=
,解得R=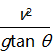 ,故A错误;根据牛顿第二定律得mgtan θ=m
,故A错误;根据牛顿第二定律得mgtan θ=m![]() ,解得v=
,解得v=![]() ,与质量无关,故B错误;若速度大于规定速度,重力和支持力的合力不够提供向心力,此时外轨对火车有侧压力,轮缘挤压外轨,故C正确;若速度小于规定速度,此时内轨对火车有侧压力,轮缘挤压内轨,故D错误。
,与质量无关,故B错误;若速度大于规定速度,重力和支持力的合力不够提供向心力,此时外轨对火车有侧压力,轮缘挤压外轨,故C正确;若速度小于规定速度,此时内轨对火车有侧压力,轮缘挤压内轨,故D错误。
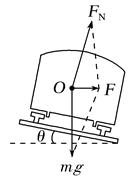
【针对训练1】 (2021·石家庄精英中学高一月考)在高速公路的拐弯处,通常路面都是外高内低。如图所示,在某路段汽车向左拐弯,司机左侧的路面比右侧的路面低一些。汽车的运动可看作水平面内半径为R的圆周运动。设内外路面高度差为h,路基的水平宽度为d,路面的宽度为L。已知重力加速度为g。要使车轮与路面之间的横向摩擦力(即垂直于前进方向)等于零,则汽车转弯时的车速应等于( )

A.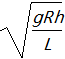 B.
B.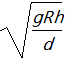
C.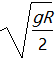 D.
D.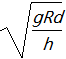
【答案】 B
【解析】 设路面的倾角为θ,作出汽车的受力图,如图所示。根据圆周运动规律得mgtan θ=m![]() ,又由数学知识得到tan θ=
,又由数学知识得到tan θ=![]() ,联立解得v=
,联立解得v=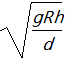 ,B正确,A、C、D错误。
,B正确,A、C、D错误。
自主探究(二) 汽车过拱形桥及航天器中的失重现象
1.拱形桥问题
(1)汽车过拱形桥(如图甲)
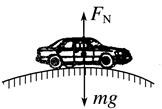
甲
汽车在最高点满足关系:
mg-FN=m![]() ,即FN=mg-m
,即FN=mg-m![]() 。
。
①当v=![]() 时,FN=0。
时,FN=0。
②当0≤v<![]() 时,0<FN≤mg。
时,0<FN≤mg。
③当v>![]() 时,汽车将脱离桥面做平抛运动,易发生危险。
时,汽车将脱离桥面做平抛运动,易发生危险。
说明:汽车通过拱形桥的最高点时,向心加速度向下,汽车对桥的压力小于其自身的重力,而且车速越大,压力越小,此时汽车处于失重状态。
(2)汽车过凹形桥(如图乙)
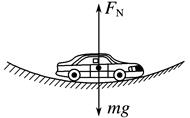
乙
汽车在最低点满足关系:
FN-mg=![]() ,即FN=mg+
,即FN=mg+![]() 。
。
说明:汽车通过凹形桥的最低点时,向心加速度向上,而且车速越大,压力越大,此时汽车处于超重状态。由于汽车对桥面的压力大于其自身重力,故凹形桥易被压垮,因而实际中很少见到凹形桥。
2.航天器中的失重现象
(1)质量为M的航天器在近地轨道运行时,航天器的重力提供向心力,满足关系:Mg=M![]() ,则v=
,则v=![]() 。
。
(2)设航天员的质量为m,航天员受到的座舱的支持力为FN,则mg-FN=m![]() 。
。
当v=![]() 时,FN=0,即航天员处于完全失重状态。
时,FN=0,即航天员处于完全失重状态。
(3)绕地球做匀速圆周运动的航天器内,任何物体都处于完全失重状态。
【例2】 (2021·北京师大附中高一期末)有一辆质量为800 kg的小汽车驶上圆弧半径为50 m的拱桥。取g=10 m/s2,求:

(1)若汽车到达桥顶时速度为5 m/s,桥对汽车的支持力FN的大小;
(2)若汽车经过桥顶时恰好对桥顶没有压力而腾空,汽车此时的速度大小v;
(3)已知地球半径R=6 400 km,现设想一辆沿赤道行驶的汽车,若不考虑空气的影响,也不考虑地球自转,那它开到多快时就可以“飞”起来。
【答案】 (1)7 600 N (2)10![]() m/s (3)8 000 m/s
m/s (3)8 000 m/s
【解析】 (1)以汽车为研究对象,由牛顿第二定律得
mg-FN=m![]() ,代入数据解得FN=7
600 N。
,代入数据解得FN=7
600 N。
(2)当FN=0时,有mg=m![]()
得v=![]() =10
=10![]() m/s。
m/s。
(3)当v=![]() 时汽车就会“飞”起来,将R=6.4×106
m代入得v=8 000 m/s。
时汽车就会“飞”起来,将R=6.4×106
m代入得v=8 000 m/s。
【例3】 在“天宫二号”中工作的景海鹏和陈冬可以自由悬浮在空中,处于失重状态,下列分析正确的是( )
A.失重就是航天员不受力的作用
B.失重的原因是航天器离地球太远,从而摆脱了地球引力的束缚
C.失重是航天器独有的现象,在地球上不可能存在失重现象
D.正是由于引力的存在,才使航天员有可能做环绕地球的圆周运动
【答案】 D
【解析】 航天器和航天员在太空中受到的引力提供向心力,使航天器和航天员做环绕地球的圆周运动,故A错误,D正确;失重时航天员仍然受到地球引力作用,故B错误;失重是普遍现象,任何物体只要有竖直向下的加速度,就会处于失重状态,故C错误。
【针对训练2】 (2021·广东佛山一中高一检测)如图,是用模拟实验来研究汽车通过拱形桥的最高点时对桥面的压力。在较大的平直木板上相隔一定距离钉几个钉子,将三合板弯曲成拱桥形卡入钉子内形成拱形桥,三合板上表面事先铺上一层牛仔布以增加摩擦,这样玩具车就可以在桥面上跑起来了。把这套系统放在电子秤上做实验,关于实验中电子秤的示数下列说法正确的是( )

A.玩具车静止在拱桥顶端时的示数小一些
B.玩具车运动通过拱桥顶端时的示数大一些
C.玩具车运动通过拱桥顶端时处于超重状态
D.玩具车运动通过拱桥顶端时速度越大(未离开拱桥),示数越小
【答案】 D
【解析】 玩具车通过拱桥顶端时处于失重状态,速度越大电子秤示数越小,故选项D正确。
自主探究(三) 离心运动
■情境导入
公路拐弯处都设置限速,其速度数值要小于在平直公路上行驶的速度;赛车场设计的车道外高内低,请分析它们其中包含的物理原理?

答案 拐弯时靠汽车所受地面摩擦力提供向心力,由Ff=m![]() 知在转弯半径一定时,速度越大,所需向心力也越大,大于最大静摩擦力Fmax时汽车将做离心运动而造成事故,故汽车转弯应设定最高速度。赛车场外高内低,靠重力和支持力的合力提供向心力可获得更大的转弯速度。
知在转弯半径一定时,速度越大,所需向心力也越大,大于最大静摩擦力Fmax时汽车将做离心运动而造成事故,故汽车转弯应设定最高速度。赛车场外高内低,靠重力和支持力的合力提供向心力可获得更大的转弯速度。
■归纳拓展
1.离心运动的实质:离心运动是物体逐渐远离圆心的一种物理现象,它的本质是物体惯性的表现。做圆周运动的物体,总是有沿着圆周切线方向飞出去的倾向,之所以没有飞出去,是因为向心力的作用。
2.离心运动的条件:提供向心力的外力突然消失或者外力不能提供足够大的向心力。
3.离心运动、近心运动的判断:物体做圆周运动、离心运动还是近心运动,由实际提供的向心力的合力F与所需向心力(m![]() 或mω2r)的大小关系决定。
或mω2r)的大小关系决定。
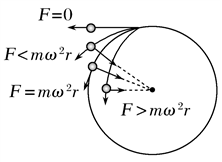
(1)若F=mω2r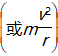 ,即“提供”等于“需要”,物体做圆周运动。
,即“提供”等于“需要”,物体做圆周运动。
(2)若F>mω2r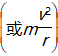 ,即“提供”大于“需要”,物体做半径变小的近心运动。
,即“提供”大于“需要”,物体做半径变小的近心运动。
(3)若F<mω2r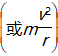 即“提供”小于“需要”,物体做半径变大的离心运动。
即“提供”小于“需要”,物体做半径变大的离心运动。
(4)若F=0,物体沿切线飞出,逐渐远离圆心。
【例4】 (2021·黑龙江大庆十中高一检测)如图所示,光滑水平面上,小球m在拉力F作用下做匀速圆周运动,若小球运动到P点时,拉力F发生变化,关于小球运动情况的说法错误的是( )
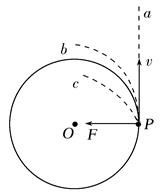
A.若拉力突然消失,小球将沿轨迹Pa做离心运动
B.若拉力突然变小,小球将沿轨迹Pa做离心运动
C.若拉力突然变小,小球将可能沿轨迹Pb做离心运动
D.若拉力突然变大,小球将可能沿轨迹Pc做近心运动
【答案】 B
【解析】 由F=![]() 知,拉力变小,F提供的向心力不足,R变大,小球做离心运动,故选项C正确,B错误;反之,F变大,小球做近心运动,选项D正确;当F突然消失时,小球将沿该点的切线飞出做直线运动,选项A正确。
知,拉力变小,F提供的向心力不足,R变大,小球做离心运动,故选项C正确,B错误;反之,F变大,小球做近心运动,选项D正确;当F突然消失时,小球将沿该点的切线飞出做直线运动,选项A正确。
【针对训练3】 (2021·山东临沂市高一检测)如图所示是一种娱乐设施“魔盘”,画面反映的是旋转魔盘转速较大时盘中人的情景。甲、乙、丙三位同学看了图后发生争论,甲说:“图画错了,做圆周运动的物体受到向心力的作用,魔盘上的人应该向中心靠拢。”乙说:“图画得对,因为旋转的魔盘给人离心力,所以人向盘边缘靠拢。”丙说:“图画得对,当盘对人的摩擦力不能满足人做圆周运动的向心力时,人会逐渐远离圆心。”这三位同学的说法正确的是( )

A.甲 B.乙
C.丙 D.都有道理
【答案】 C
【解析】 当向心力不足时,物体会做离心运动,离心力是不存在的,A、B、D错误,C正确。
1.(火车或汽车转弯问题)(2021·浙江温州九校高一期末)一质量为2.0×103 kg的汽车在水平公路上行驶,路面对轮胎的径向最大静摩擦力为1.4×104 N,当汽车经过半径为80 m的弯道时,下列判断正确的是( )
A.汽车转弯时所受的力有重力、弹力、摩擦力和向心力
B.汽车转弯的速度为20 m/s时所需的向心力为1.4×104 N
C.汽车转弯的速度为20 m/s时汽车会发生侧滑
D.汽车能安全转弯的向心加速度不超过7.0 m/s2
【答案】 D
【解析】 汽车转弯时受到重力、地面的支持力以及地面的摩擦力,不存在向心力,向心力是根据力的效果命名的,A错误;当最大静摩擦力提供向心力时,速度为临界速度,大于这个速度则发生侧滑,根据牛顿第二定律可知Fmax=m![]() ,解得
,解得
v=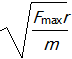 =20
=20![]() m/s,所以汽车转弯的速度为20 m/s时,所需的向心力小于1.4×104
N,汽车不会发生侧滑,B、C错误;汽车能安全转弯的向心加速度a=
m/s,所以汽车转弯的速度为20 m/s时,所需的向心力小于1.4×104
N,汽车不会发生侧滑,B、C错误;汽车能安全转弯的向心加速度a=![]() =
=![]() m/s2=7 m/s2,即汽车能安全转弯的向心加速度不超过7.0 m/s2,D正确。
m/s2=7 m/s2,即汽车能安全转弯的向心加速度不超过7.0 m/s2,D正确。
2.(火车或汽车转弯问题)(2021·陕西长安一中高一月考)如图所示,在自行车比赛中,运动员以速度v在倾角为θ的赛道上做匀速圆周运动。已知运动员的质量为m,做圆周运动的半径为R,重力加速度为g,则下列说法正确的是( )

A. 将运动员和自行车看作一个整体,整体受重力、支持力、摩擦力和向心力的作用
B.运动员受到的合力为![]() ,是一个恒力
,是一个恒力
C.若运动员加速,则可能沿斜面上滑
D.若运动员加速,则一定沿斜面下滑
【答案】 C
【解析】 向心力是效果力,可以由单个力提供,也可以由几个力的合力提供,或者由某个力的分力提供,不是性质力,因此,将运动员和自行车看作一个整体后,整体应受重力、支持力和摩擦力,故A错误;由题意可知,运动员做线速度大小为v,半径为R的匀速圆周运动,故运动员受到的合力提供向心力,则有F合=![]() ,合力方向总是沿着半径指向圆心,运动员受到的合力是一个变力,故B错误;如果运动员加速速度增大时,需要的向心力增大,当向心力“供”小于“需”,运动员将会做离心运动,可能沿斜面上滑,故C正确,D错误。
,合力方向总是沿着半径指向圆心,运动员受到的合力是一个变力,故B错误;如果运动员加速速度增大时,需要的向心力增大,当向心力“供”小于“需”,运动员将会做离心运动,可能沿斜面上滑,故C正确,D错误。
3.(汽车过拱形桥问题)(2021·深州中学高一月考)公路在通过小型水库的泄洪闸的下游时,常常要修建凹形桥,也叫“过水路面”。如图所示,汽车通过凹形桥的最低点时( )
A.车对桥的压力等于汽车的重力
B.车对桥的压力小于桥对汽车的支持力
C.汽车所需的向心力就是地面对车的支持力
D.为了防止爆胎,车应低速驶过
【答案】 D
【解析】 在最低点,根据牛顿第二定律知,地面对车的支持力与车的重力的合力提供了向心力,设桥对车的支持力为FN,有FN-mg=m![]() ,所以FN>mg,根据牛顿第三定律得车对桥的压力大于重力,A、B、C错误;为了防止爆胎,应减小桥对车的支持力FN,FN=m
,所以FN>mg,根据牛顿第三定律得车对桥的压力大于重力,A、B、C错误;为了防止爆胎,应减小桥对车的支持力FN,FN=m![]() +mg,所以应该减小速度,D正确。
+mg,所以应该减小速度,D正确。
4.(离心运动)下列事例与离心现象无关的是( )
A.离心沉淀器
B.标枪运动员掷出的标枪
C.转动伞柄可将雨伞上的水甩出
D.家用洗衣机的甩干筒用于干燥衣物
【答案】 B
【解析】 离心沉淀器的原理,属于离心现象; 标枪运动员掷出的标枪做斜上抛运动,受到恒力的作用,所以投出的标枪的运动不属于离心现象;通过旋转雨伞来甩干伞上的雨滴,当转动加快时雨滴所需要的向心力增加,当超过雨伞对雨滴的吸附力时,雨滴做离心运动; 脱水桶高速转动时,需要的向心力大于水和衣服之间的附着力时,水做离心运动被从衣服上甩掉,属于离心现象,故选B。





