(1)若合加速度不变，则为匀变速运动；若合加速度(大小或方向)变化，则为非匀变速运动。

(2)若合加速度的方向与合初速度的方向在同一直线上，则为直线运动，否则为曲线运动。

2. 小船过河

(1)当船速大于水速时

①船头的方向垂直于水流的方向则小船过河所用时间最短，有：t＝

②合速度垂直于河岸时，航程s最短，有：s＝d   

(2)当船速小于水速时

①船头的方向垂直于水流的方向时，所用时间最短，t＝

②合速度不可能垂直于河岸，最短航程s＝d×

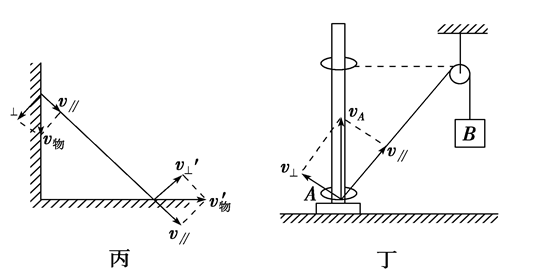
3．绳（杆）端物体速度分解

分解不沿绳（杆）那个速度为沿绳(杆)和垂直于（杆），沿绳（杆）方向速度大小相等。

4．圆周运动

（1）圆周运动各物理量间的关系

（2）三类传动方式及特点

①皮带传动：如图甲、乙所示，皮带与两轮之间无相对滑动时，两轮边缘线速度大小相等，即v_A＝v_B。

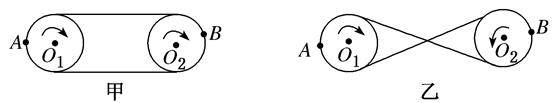
②摩擦传动和齿轮传动：如图丙、丁所示，两轮边缘接触，接触点无打滑现象时，两轮边缘线速度大小相等，即v_A＝v_B。

③同轴传动：如图戊、己所示，绕同一转轴转动的物体，角速度相同，ω_A＝ω_B，由v＝ωr知v与r成正比。

(3)圆周运动模型

①水平面内的圆周运动，向心力为F＝mgtan θ，方向水平指向圆心。

②竖直面内的圆周运动

①绳或内轨、水流星最高点的最小速度为，最低点最小速度为，最高、最低两点拉（压）力之差为6mg。

②小球在“杆”模型最高点v_min＝0，v_临＝，v＞v_临，杆对小球有向下的拉力；v＝v_临，杆对小球的作用力为零；v＜v_临，杆对小球有向上的支持力。

③如图所示，小球要通过最高点，小球最小下滑高度为H=2.5R。

④绳一端固定一端系一小球，忽略空气阻力，从水平位置无初速度释放小球下摆到最低点：绳上拉力F_T＝3mg，向心加速度a＝2g，与绳长无关。（半径不同的光滑圆轨道同样的结论）。

 

⑤圆锥摆周期公式

(h为绳的悬点与圆周运动的圆面的高度)

5、平抛运动

（1）水平方向速度：  

（2）竖直方向速度：

（3）水平方向位移：

（4）竖直方向位移：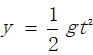

（5）运动时间：

（6）合速度：

合速度方向与水平夹角：

（7）合位移：

位移方向与水平夹角：

（8）水平方向加速度：；竖直方向加速度：

（9）与的关系为

6、万有引力与航天

(1)某星球表面处重力加速度：: g＝。（R为天体半径，适用条件：忽略天体自转的影响）

(2)距离该天体表面h处重力加速度：

g′＝＝(h为)

(3)人造卫星（万有引力提供向心力）：

G＝m＝mω²r＝mr＝ma＝mg′

速度: ，周期: ，加速度：<g（r增大，a减小，v减小，ω减小，T增大）。

（4）第一宇宙速度：v₁＝＝＝7.9 km/s，，

近地表面的人造卫星：r＝R＝6.4×10⁶ m，v_运＝v₁，T＝2π＝84.6分钟

(5)同步卫星：周期T＝24小时，离地高度：h＝5.6R＝36000km，v＝3.1 km/s

(6)月球：周期T＝27.32天。

(7)黄金替换式：GM＝gR²(），

(8)不忽略地球自转的影响，在地球两极：

在赤道上的物体：

(9)行星密度：ρ＝，式中T为绕行星表面运转的卫星的周期。

(10)卫星变轨：  , ,

(11)恒星质量： 或

(12)引力势能：，卫星动能：，卫星机械能：

同一卫星在半长轴为a=R的椭圆轨道上运动的机械能，等于半径为R圆周轨道上的机械能。

卫星由近地点到远地点，万有引力做负功。

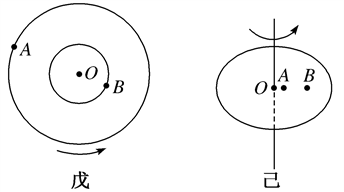
7．双星模型

(1)定义：绕公共圆心转动的两个星体组成的系统，我们称之为双星系统，如图所示．

 (2)特点：

①各自所需的向心力由彼此间的万有引力相互提供，即

对于m_1：＝m₁ωr₁

对于m_2：＝m₂ωr₂

②两颗星的周期及角速度都相同，即

T₁＝T₂，ω₁＝ω₂

③两颗星的半径与它们之间的距离关系为：r₁＋r₂＝L

(3)两颗星到圆心的距离r₁、r₂与星体质量成反比，即＝

8．多星模型

(1)定义：所研究星体的万有引力的合力提供做圆周运动的向心力，除中央星体外，各星体的角速度或周期相同．

(2)三星模型：

①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图3甲所示)．

②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)．

（3）四星模型

①其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙所示)。

②另一种是三颗恒星始终位于正三角形的三个顶点上，另一颗位于中心O，外围三颗星绕O做匀速圆周运动(如图丁所示)。

返回目录页：手机端   电脑端

第一步：关注公众号“三峡教育资讯”

第二步：回复关键词：三峡教育资讯  

即可获取完整版资源下载地址！